Как сделать проверку матрицы в excel?

Транспонирование матрицы в Excel

Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т
.

Пусть дана матрица А
размерностью 3х4
, с помощью функции =ТРАНСП()
вычислим транспонированную матрицу А Т
, причем размерность этой матрицы будет 4х3
.

Выделим диапазон Н3:
J
6
, в который будут введены значения транспонированной матрицы.

На вкладке Формулы
выберем Вставить функцию,
выберем категорию Ссылки и массивы
— функция ТРАНСП
— ОК
.

В диалоговом окне Аргументы функции
указываем диапазон массива В3:Е5
А
Shift
+
Ctrl
и щелкаем левой кнопкой мыши по кнопке ОК
.

ВАЖНО.
Если просто нажать ОК
, то программа вычислит значение только первой ячейки диапазона матрицы А Т

Нажмите для увеличения

Мы получили транспонированную матрицу.

2.7. Регрессия

Векторизуем внутренний цикл (2-й шаг)

1. Компиляторы нынче умные пошли (не все!), и вполне справляются с задачей автовекторизации простых циклов. Уже в 1-м варианте компилятор фактически задействовал инструкции AVX2/FMA, потому ручная оптимизация не дала нам практически никаких преимуществ.
2. Скорость расчетов в данном случае упирается не в вычислителные возможности процессора, а в скорость загрузки и выгрузки данных. В данном случае процессору для задействования 2 256-bit FMA блоков требуется загрузить 4 и выгрузить 2 256-bit вектора за такт. Это в два раза превышает даже пропускную способность L1 кеша процессора (512/256 bit), не говоря уже о пропускной способности памяти, которая еще на порядок меньше (64-bit на канал)).

Основные свойства матричного произведения

В двух словах. Умножение матриц:

1. Некоммутативно: $A\cdot B\ne B\cdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $A\cdot B=B\cdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;
2. Ассоциативно: $\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.
3. Дистрибутивно: $A\cdot \left( B+C \right)=A\cdot B+A\cdot C$ и $\left( A+B \right)\cdot C=A\cdot C+B\cdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.

А теперь — всё то же самое, но более подробно.

Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.

Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:

\\cdot \left=\left\]

Но если поменять матрицы местами, то получим совсем другой результат:

\\cdot \left=\left\]

Получается, что $A\cdot B\ne B\cdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=\left$ и $B=\left$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $\left$ и $\left$ вполне себе согласованы в указанном порядке, но те же матрицы $\left$ и $\left$, записанные в обратном порядке, уже не согласованы. Печаль.:(

Тем не менее, умножение матриц ассоциативно:

\

Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.

В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $\left$. Множество всех таких матриц обозначается ${{M}^{n}}$ (т.е. записи $A=\left$ и \ означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.

Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:

\

Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)

Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.

Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?

2.8. Критическая ошибка в Excel 2003

В Excel 2003 функции TREND и
LINEST при определенных
условиях дают неверный результат.

Так происходит когда одновременно:

• среднее значение по каждой переменной в матрице
  предикторов X равно нулю;

• среднее значение отклика Y
  не равно нулю.

На показан как раз такой
случай: средние значения по всем столбцам матрицы Xc
равны нулю, а среднее по столбцу Yc отлично от нуля..

Пример 
 

Рис.37 Ошибка в регрессионных функциях Excel
2003

Ситуацию можно исправить, применяя функцию
TREND к
центрированным значениям отклика, с последующей коррекцией результата.
Для этого можно использовать формулу
=TREND(Yc-ym,
Xc)+ym, применение которой показано на том же рисунке.

Удивительно, но эта ошибка не была замечена
пользователями. Однако в новой версии 2007 она исправлена.  

Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа:
при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.

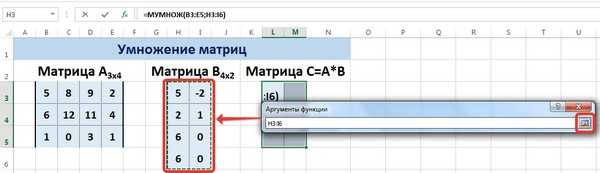
Умножение матриц в Excel

Условие задачи:

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Формулы массива в Excel

Под массивом обычно понимают набор данных, объединенных в группу. Массивы бывают одномерные (элементы массива образуют строку или столбец) или двумерные (матрица). Легко сообразить, что почти в любой таблице Excel при желании можно найти один или несколько таких массивов:

Формулы массива в Excel – это специальные формулы для обработки данных из таких массивов. Формулы массива делятся на две категории – те, что возвращают одно значение и те, что дают на выходе целый набор (массив) значений. Рассмотрим их на простых примерах…

Пример 1. Классика жанра – товарный чек

Задача: рассчитать общую сумму заказа. Если идти классическим путем, то нужно будет добавить столбец, где перемножить цену и количество, а потом взять сумму по этому столбцу. Если же применить формулу массива, то все будет гораздо красивее:

1. выделяем ячейку С7
2. вводим с клавиатуры =СУММ(
3. выделяем диапазон B2:B5
4. вводим знак умножения (звездочка)
5. выделяем диапазон C2:C5 и закрываем скобку функции СУММ – в итоге должно получиться так:
6. чтобы Excel воспринял нашу формулу как формулу массива жмем не Enter, как обычно, а Ctrl + Shift + Enter

Вуаля!

Т.е. Excel произвел попарное умножение элементов массивов B2:B5 и C2:C5 и образовал новый массив стоимостей (в памяти компьютера), а затем сложил все элементы этого нового массива.

Обратите внимание на фигурные скобки, появившиеся в формуле – отличительный признак формулы массива. Вводить их вручную с клавиатуры бесполезно – они автоматически появляются при нажатии Ctrl + Shift + Enter

Пример 2. Разрешите Вас… транспонировать?

При работе с таблицами часто возникает необходимость поменять местами строки и столбцы, т.е. развернуть таблицу на бок, чтобы данные, которые раньше шли по строке, теперь располагались в столбцах и наоборот. В математике такая операция называется транспонированием. При помощи формулы массива и функции ТРАНСП (TRANSPOSE) это делается на раз.

Допустим, имеем двумерный массив ячеек, который хотим транспонировать.

• Выделяем диапазон ячеек для размещения транспонированной таблицы. Поскольку исходный массив ячеек был 8 строк на 2 столбца, то надо выделить диапазон пустых ячеек размером 2 строки на 8 столбцов.
• вводим функцию транспонирования =ТРАНСП(   
• в качестве аргумента функции выделяем наш массив ячеек A1:B8

жмем Ctrl + Shift + Enter и получаем “перевернутый массив” в качестве результата:

Редактирование формулы массива

Если формула массива расположена не в одной ячейке (как в Примере 1), а в нескольких ячейках (как в Примере 2), то Excel не позволит редактировать или удалить одну отдельно взятую формулу (например в ячейке D10) и выдаст предупреждающее сообщение Невозможно изменить часть массива.

Для редактирования формулы массива необходимо выделить весь диапазон (A10:H11 в нашем случае) и изменить формулу в строке формул (или нажав F2). Затем необходимо повторить ввод измененной формулы массива, нажав сочетание клавиш Ctrl + Shift + Enter.

Excel также не позволит свободно перемещать ячейки, входящие в формулу массива или добавлять новые строки-столбцы-ячейки в диапазон формулы массива (т.е. в диапазон A10:H11 в нашем случае)

Пример 3. Таблица умножения

Вспомните детство, школу, свою тетрадку по математике… На обороте тетради на обложке было что? Таблица умножения вот такого вида:

При помощи формул массива она вся делается в одно движение:

1. выделяем диапазон B2:K11
2. вводим формулу =A2:A11*B1:K1
3. жмем Ctrl + Shift + Enter, чтобы Excel воспринял ее как формулу массива

и получаем результат:

Пример 4. Выборочное суммирование

Посмотрите как при помощи одной формулы массива красиво и легко выбираются данные по определенному товару и заказчику:

 В данном случае формула массива синхронно пробегает по всем элементам диапазонов C3:C21 и B3:B21, проверяя, совпадают ли они с заданными значениями из ячеек G4 и G5. Если совпадения нет, то результат равенства ноль, если совпадение есть, то единица. Таким образом суммы всех сделок, где заказчик не ANTON и товар не Boston Crab Meat умножаются на ноль и суммируются только нужные заказы.

Видеоурок

Учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Найти определитель матрицы 3*3
можно быстро по правилу треугольника

Определители обозначают следующими знаками

Примеры вычисления определителей

Пример 1.
Найти определитель матрицы

Определитель равен 11. Приведенная схема пригодиться Вам для вычисления определителя матрицы 3 * 3. Все что Вам нужно — подставить свои значения.

Пример 2.
Вычислить определитель матрицы Решение:
В целях научить Вас чему-то новому, найдем определитель матрицы по правилу Саррюса.

Схема вычислений приведена выше поэтому копировать ее не будем, а лишь распишем в деталях. Для этого дописываем к стандартному определителю два первых столбца и выполняем следующие расчеты.

В результате вычислений определитель равен нулю.

Пример 3.
Найти определитель матрицы 3*3 Решение:
Применяем правило треугольника для нахождения определителя

Определитель равен -161.

Пример 4.
Вычислить определитель матрицы
Решение:
Находим определитель матрицы 3*3 по правилу треугольников

Пример 5.
Найти определитель матрицы
Решение:
Матрица имеет несколько нулевых элементов. Такие матрицы называют разреженными. Для уменьшения количества операций вычислим определитель через алгебраические дополнения
ко второму строки или столбца.

Проще уже не может быть.

Пример 6.
Доказать что определитель матрицы А
равен 3Решение:
Матрица содержит два нулевых элементы, поэтому можем найти определитель через алгебраические дополнения. Разложим определитель по элементам первого столбца.

Определитель равен 3 что и требовалось доказать.

Пример 7.
Найти определитель матрицы
Решение:
По предварительной схеме определитель матрицы вычисляем через алгебраические дополнения первой строки или третьего столбца. выполняем вычисления

Определитель равен 39.

Пример 8.
При каких значениях параметра а
определитель матрицы равен нулю
Решение:
По правилу треугольников находим определитель По условию приравниваем определитель к нулю и находим параметр

Параметры при которых определитель обращается в нуль уровне a=-3;a=3
.

Пример 9.
Найти определитель матрицы
Решение:
Найдем определитель матрицы по правилу треугольников и через алгебраические дополнения. По первой схеме получим Теперь разложим с помощью алгебраических дополнений, например, третьим столбцом. Он удобен тем, что содержит самые элементы матрицы. Находим определитель Сравнением количества расчетов убеждаемся, что в таких случаях целесообразнее использовать правило треугольников. Вычисления проще и меньше вероятность сделать ошибку.

Для разреженных матриц или большего порядка блочных стоит применять расписание определителя по строке или столбцу. И напоследок бонус от нас — калькулятор YukhymCalc.

С его помощью Вы легко проверите правильность исчисления основных операций с матрицами, а также сможете найти определитель матрицы и обратную матрицу. Для матриц 3*3 используется правило треугольников, для 4*4 — расписание определителя через элементы первой строки. Меню довольно простое и интуитивно понятное. Определитель 7 задачу через матричный калькулятор иметь следующий вид

Как видите преимущество матричного калькулятора перед другими, в том числе онлайн калькуляторами, в том, что Вы видите все промежуточные операции

А это важно для проверки и контроля ошибок

Используйте приведенные схемы вычислений определителей в обучении. Если возникают трудности в вычислениях и есть возможность, то можете проверить найдены определители калькулятором. Скачать матричный калькулятор YukhymCalc
Вы можете без регистрации по этой ссылке.

Равенство матриц

Сложение матриц

1+ 1 2+ 3 3+ 0

0 + 0 2

− 2

− 2 11

C= A+ B=

1+ 11

4 + 4

1+ 10 2

Свойства сложения матриц

A +
B=
B+
A;

Умножение матрицы на число

B = 3*A =

Свойства умножения матриц

(αi
β)
i
A
=
αi
(βi
B
)
.

Вычитание матриц

	A −B =A +(−1 ) iB
A = 0 2 1 ,B = 0	− 2 11 .
			10 0 4
1− 1 2− 3	3 − 0		− 1 3
C =A −B =0 −0 2 +2	1− 11			− 10 .
1− 10 2− 0	4 − 4	− 9 2

Произведение двух матриц

a1 n

ai 2

ai 1

… … … … … …

bn 2

bn 1

n× p

mn m × n

называется матрица

		c 12…	c 1p
	C = 21
	cm 1			c mp
	c m 2 …
					m× p
c ij= ∑ a ik* b kj= a i1 * b 1 j+ … + a in* b nj,	i = 1, 2,…,m ;j = 1, 2,…,p ,
k = 1
т.е. элемент матрицы c ij	Стоящий на пересечении i	– строки и j -столбца равен сумме
произведений элементов i	– строки матрицы A на соответствующие элементыj -столбца

		2× 2			2× 3
2i 1+ 3i 4 2i 2+	3i 5 2i 3	3 i6
C = Ai B=

3 .3 . Пример макроса

Решение матриц в Excel

1.10. Построение графиков

В Excel можно строить диаграммы разных типов. Но для нас
интересны только два вида: диаграмма рассеяния (scatter) и  график (line).
Пример диаграммы рассеяния приведен на Рис. 24 .

Рис.24
Диаграмма рассеяния

Диаграммы такого типа используются для построения графиков
счетов, зависимостей «измерено-предсказано», и т.п. От линейных графиков
они отличаются равноправием обеих осей. В линейных графиках ось абсцисс
предназначена только для отображения категорийных переменных, т.е.
величин, в которых важна не их величина, а порядок следования. Поэтому
линейные графики подходят для представления зависимостей от числа
главных компонент, например, для изображения того, как величины RMSEC и
RMSEP меняются при усложнении модели.

Методы построения  графиков в версиях 2003 и 2007 сильно
отличаются. Поэтому мы не будем на этом останавливаться, предоставив эту
тему для

самостоятельного изучения.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.  

Синтаксис 

TREND(known_y’s
)

Примечания 

• Вектор
  known_y’s должен занимать один столбец,
  тогда каждый столбец матрицы массива known_x’s
  интерпретируется как отдельная переменная;

• Если
  аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
  такого же размера, как и known_y’s;

• Матрица
  новых значений new_x’sдолжна иметь столько же столбцов
  (переменных), как и матрица known_x’s;

• Если
  аргумент new_x’sопущен, то предполагается, что он совпадает с
  массивом known_x’s.
  Результат является вектором, в котором число строк равно
  числу строк в массиве new_x’s.

Пример 
 

Рис.34 Функция TREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER. 

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией  

y=b+m₁x₁+…+m_J x_J+e

Синтаксис 

LINEST(known_y’s
)

Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания 

• LINEST – это
  очень плохо сконструированная функция, очень неудобная в
  практическом применении;

• Примечания,
  представленные в описании функции полностью применимы к
  функции LINEST.

Пример 
 

Рис.36 Функция LINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER. 

Простые операции с матрицами

Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы. 

И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.

Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре
Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений

Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

Пример умножения матрицы на число

Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок. 

️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы
Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т»
Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил

3.6. Установка надстроек