Вычисление суммы ряда в Excel
Та же функция РЯД.СУММ работает со степенными рядами (одним из вариантов функциональных рядов). В отличие от числовых, их аргументы являются функциями.
Функциональные ряды часто используются в финансово-экономической сфере. Можно сказать, это их прикладная область.
Например, положили в банк определенную сумму денег (а) на определенный период (n). Имеем ежегодную выплату х процентов. Для расчета наращенной суммы на конец первого периода используется формула:
На конец второго и последующих периодов – вид выражений следующий:
S2 = a (1 + x) 2 ; S3 = a (1 + x) 2 и т.д.
Чтобы найти общую сумму:
Sn = a (1 + x) + a (1 + x) 2 + a (1 + x) 3 + … + a (1 + x) n
Частичные суммы в Excel можно найти с помощью функции БС().
Исходные параметры для учебной задачи:
Используя стандартную математическую функцию, найдем накопленную сумму в конце срока сумму. Для этого в ячейке D2 используем формулу: =B2*СТЕПЕНЬ(1+B3;4)
![]()
Теперь в ячейке D3 решим эту же задачу с помощью встроенной функции Excel: =БС(B3;B1;;-B2)
![]()
Результаты одинаковые, как и должно быть.
Как заполнить аргументы функции БС():
![]()
- «Ставка» – процентная ставка, под которую оформлен вклад. Так как в ячейке В3 установлен процентный формат, мы в поле аргумента просто указали ссылку на эту ячейку. Если было бы указано число, то прописывали бы его сотую долю (20/100).
- «Кпер» – число периодов для выплат процентов. В нашем примере – 4 года.
- «Плт» – периодические выплаты. В нашем случае их нет. Поэтому поле аргумента не заполняем.
- «Пс» – «приведенная стоимость», сумма вклада. Так как мы на время расстаемся с этими деньгами, параметр указываем со знаком «-».
Таким образом, функция БС помогла найти нам сумму функционального ряда.
В Excel есть и другие встроенные функции для нахождения разных параметров. Обычно это функции для работы с инвестиционными проектами, ценными бумагами и амортизационными платежами.
Необходимый признак сходимости числового ряда
Теорема. Если ряд сходится, то предел его общего члена при
равен нулю:
(17)
Следствие. Если предел общего члена ряда при
не равен нулю, то ряд расходится.
Пример 11. Используя необходимый признак сходимости, исследовать сходимость числового ряда
Решение. Общий член ряда
Найдём его предел при
Следовательно, данный ряд расходится.
Пример 12. Используя необходимый признак сходимости, исследовать сходимость числового ряда
Решение. Найдём предел общего члена ряда при
Так как (предел общего
члена не равен нулю), данный ряд расходится.
Установить сходимость ряда самостоятельно, а затем посмотреть решение
Пример 13. Используя необходимый признак сходимости,
установить, сходится ли ряд
.
Пример 14. Установить, сходится ли ряд
.
Пример 15. Записать первые пять членов числового ряда
и установить, сходится ли этот ряд.
Решение. Пять первых членов данного числового ряда:
Найдём предел общего члена ряда при
,
применяя дважды правило Лопиталя:
Так как (предел общего
члена равен нулю), данный ряд сходится.
Мы выяснили, что если числовой ряд сходится, то предел его общего члена равен нулю, а значит, выполняется условие (17).
Однако выполнение условия (17) не гарантирует сходимости числового ряда, оно не является достаточным для этого. Есть расходящиеся ряды, пределы общих членов которых при
равны нулю.
Примером такого ряда служит ряд (4):
который называется гармоническим. Последовательность его частичных сумм
монотонно возрастает, поскольку члены ряда положительны. Покажем, что она возрастает неограниченно. Для этого члены гармонического ряда, начиная с третьего, объединим в группы:
В первую включим два члена (3-й и 4-й), во вторую
члена (с 5-го по 8-й), в третью
членов (с 9-го по 16-й) и т.д, каждый раз увеличивая вдвое число членов в группе. Таких групп, очевидно, бесконечное множество. Если заменить члены ряда в каждой группе их последними членами, то сумма членов этой группы уменьшится и тогда справедливы неравенства
Сумма членов каждой группы больше 1/2, а сумма членов, включённых в достаточно большое число групп, как угодно велика. Следовательно, последовательность частичных сумм гармонического ряда неограниченно возрастает, а ряд расходится, хотя его общий член
при
стремится к нулю.
Заметим, что частичные суммы гармонического ряда возрастают хотя и ограниченно, но медленно.
Исследование сходимости ряда обычно начинают с проверки выполнения условия (17), чтобы сразу выделить расходящиеся ряды, для которых это условие не выполняется. Однако выполнение этого условия говорит лишь о том, что ряд может сходиться. Сходится он или расходится, должно показать дополнительное исследование с помощью достаточных признаков, рассмотрение которых дано в последующих урока раздела «Ряды».
| Назад | Листать | Вперёд>>> |
Всё по теме «Ряды»
- Числовые ряды
- Признак сравнения рядов
- Признак Даламбера сходимости рядов
- Радикальный признак Коши сходимости рядов
- Интегральный признак Коши сходимости рядов
- Знакочередующиеся и знакопеременные ряды. Признак Лейбница
- Функциональные ряды
- Степенные ряды
- Ряды Фурье
Понятие сходимости числовых рядов
Если значения частичных сумм
при неограниченном возрастании n, то есть, при
стремятся к некоторому числу S, то есть имеет предел
(8)
то числовой ряд называется сходящимся.
Это число S называется суммой числового ряда.
В этом смысле можно записать такое равенство:
(9)
Пример сходящегося числового ряда:
Не для всякого числового ряда последовательность его частичных сумм
стремится к определённому пределу. Например, для ряда
частичные суммы
принимают попеременно значения 1 и 0:
Если предел последовательность частичных сумм ряда не существует, то числовой
ряд называется расходящимся. Расходящийся ряд суммы не имеет.
Пример 5. Определить частичную сумму числового ряда
,
разложив общий член ряда на элементарные дроби с помощью метода неопределённых
коэффициентов, и найти сумму ряда.
Решение. Разложим общий члена ряда на элементарные дроби:
Так как дроби равны и знаменатели равны, числители также должны быть равны:
Это равенство в силе для всех n:
Таким образом,
.
Частичная сумма ряда:
Сумма ряда:
.
Пример 6. Исследовать сходимость числового ряда (2) .
Решение. Составим частичные суммы ряда:
Представим их в виде
Нетрудно заметить закономерность в образовании частичных сумм: каждая представляет разность между единицей и дробью, числитель которой 1, а знаменатель n-й частичной суммы равен n + 1, т.е.
Найдём предел последовательности частичных сумм:
Следовательно, числовой ряд (2) сходится, его последовательность равна 1.
Исследуем сходимость числового ряда (3):
который называется геометрическим, так как его члены представляют собой члены
геометрической прогрессии, первый член которой равен a, а знаменатель q.
Рассмотрим частичную сумму этого ряда:
Она равна сумме членов геометрической прогрессии, если
те есть
Найдём предел последовательности частичных сумм геометрического ряда. Следует различать четыре возможности:
1)
2)
3)
4)
1. Если
то ,
поэтому
2. Если
то
не существует, значит и последовательность частичных сумм не имеет предела.
3. Если q =1, то получается ряд a + a + a +…+ … . Его n-я частичная сумма
при
в зависимости от знака a.
4. Если q = — 1, то получается ряд
Его частичные суммы попеременно равны a и 0:
и т.д. Но такая последовательность не имеет предела.
Мы выяснили, что геометрический ряд (3) сходится, если знаменатель меньше единицы:
причём его сумма равна
,
и расходится, если равен или больше единицы:
Пример 7. Исследовать сходимость числовых рядов:
(*)
(**)
(***)
(****)
Решение. Это геометрические ряды. Для ряда (*)
для ряда (**)
для ряда (***) q = 4/3; для ряда (****) q = — 1. Следовательно, первые два ряда сходятся, а последние два расходятся.
Пример 8. Опредедить, сходится ли числовой ряд
.
В случае положительного ответа найти его сумму.
Решение. Данный ряд является геометрическим рядом с первым членом
и
. Так как
, ряд сходится.
Сумму ряда найдём по формуле суммы геометрического ряда
.
Таким образом,
.
Знак суммы в математике как считать?
summa — итог, общее количество), результат сложения величин (чисел, функций, векторов, матриц и т. .
Как записать алгебраическую сумму?
Обратите внимание, что запись алгебраической суммы обычно упрощают: положительные числа записываются без предшествующего знака + , а отрицательные числа, стоящие в начале выражения, записываются без скобок: (-5) + (+7) = -5 + 7. заменяют на выражение: 3z — 2x — y
Что такое слагаемое в математике?
Числа при сложении называются слагаемыми. Результат сложения – сумма. сложение, слагаемые, сумма, результат сложения.
Что такое сумма чисел 2 класс?
Сложение – это объединение объектов в одно целое. Результатом сложения чисел является число, называемое суммой чисел (слагаемых). . Большее число называется уменьшаемым, меньшее – вычитаемым, результат вычитания – разностью.
Что такое разность и ее значение?
Значение разности: Разность-это то что получается при вычитание чисел. . Уменьшаемое-вычитаемое=разность. Вот оно значение разности .
Как найти алгебраическую сумму многочленов?
Для того чтобы найти алгебраическую сумму нескольких многочленов, записанную в стандартном виде, необходимо раскрыть скобки и привести подобные слагаемые. При этом, если перед скобкой стоит знак «плюс», то раскрывая скобки, знаки перед слагаемыми нужно оставить без изменений.
Построение графика функций суммы числового ряда
Построим график функций, отражающий рост капитала. Для этого нам нужно построить график функции являющейся суммой построенного ряда. За пример, возьмем те же данные по вкладу:
Дальше нам нужна функция для начисления сложных процентов – БС(). Мы узнаем будущею стоимость инвестиций при условии равных платежей и постоянной процентной ставке. Используя функцию БС(), заполним таблицу:
![]()
В первой строке показана накопленная сумма через год. Во второй – через два. И так далее.
Сделаем еще один столбец, в котором отразим прибыль:
![]()
Как мы считали – в строке формул.
На основании полученных данных построим график функций.
Выделим 2 диапазона: A5:A9 и C5:C9. Переходим на вкладку «Вставка» – инструмент «Диаграммы». Выбираем первый график:
![]()
![]()
Сделаем задачу еще более «прикладной». В примере мы использовали сложные проценты. Они начисляются на наращенную в предыдущем периоде сумму.
Возьмем для сравнения простые проценты. Формула простых процентов в Excel: =$B$2*(1+A6*B6)
![]()
Добавим полученные значения в график «Рост капитала».
![]()
Какие именно выводы сделает инвестор – очевидно.
Математическая формула частичной суммы функционального ряда (с простыми процентами): Sn = a (1 + x*n), где а – первоначальная сумма вклада, х – проценты, n – период.
Свойства сходящихся рядов.
Свойство 1.
Если ряды \(\displaystyle\sum_{n=1}^{\infty}a_{n}\) и
$$
\sum_{n=1}^{\infty}b_{n},\label{ref12}
$$
сходятся, а их суммы равны соответственно \(S\) и \(\sigma\), то при любых \(\lambda, \mu \in \mathbb{R}\) сходится ряд
$$
\sum_{n=1}^{\infty}(\lambda a_{n} + \mu b_{n}),\label{ref13}
$$
а его сумма равна
$$
\tau = \lambda S + \mu\sigma.\label{ref14}
$$
\(\circ\) Пусть \(S_{n}\), \(\sigma_{n}\) и \(\tau_{n}\) — \(n\)-е частичные суммы рядов \eqref{ref2}, \eqref{ref12} и \eqref{ref13} соответственно. Тогда \(\tau_{n} = \lambda S_{n} + \mu\sigma_{n}\). Так как \(S_{n} \rightarrow S\) и \(\sigma_{n} \rightarrow \sigma\) при \(n \rightarrow \infty\), то последовательность \(\{\tau_{n}\}\) имеет конечный предел, то есть ряд \eqref{ref13} сходится, и справедливо равенство \eqref{ref14}. \(\bullet\)
Свойство 2.
Если сходится ряд \(\displaystyle\sum_{n=1}^{\infty}a_{n}\), то при каждом \(m \in \mathbb{N}\) сходится ряд
$$
\sum_{n=m+1}^{\infty}a_{n},\label{ref15}
$$
который называют \(m\)-м остатком ряда \(\displaystyle\sum_{n=1}^{\infty}a_{n}\). Обратно: если при фиксированном \(m\) ряд \eqref{ref15} сходится, то и ряд \(\displaystyle\sum_{n=1}^{\infty}a_{n}\) также сходится.
\(\circ\) Пусть \(S_{n} = a_{1} + \ldots + a_{n}\) и \(\sigma_{k}^{(m)} = a_{m+1} + \ldots + a_{m+k}\)-соответственно \(n\)-я частичная сумма ряда \eqref{ref2} и \(k\)-я частичная сумма ряда \eqref{ref15}. Тогда
$$
S_{n} = S_{m} + \sigma_{k}^{(m)},\ \mbox{где}\ n = m + k.\label{ref16}
$$
Если ряд \eqref{ref2} сходится, то последовательность \(\{S_{n}\}\) имеет конечный предел при \(n \rightarrow \infty\), и поэтому из равенства \eqref{ref16} следует, что последовательность \(\{\sigma_{k}^{(m)}\}\), где \(m\) фиксировано, имеет конечный предел при \(k \rightarrow \infty\), то есть ряд \eqref{ref15} сходится.
Обратно: если \(m\) фиксировано и существует конечный \(\displaystyle\lim_{k \rightarrow \infty}\sigma_{k}^{(m)}\) то существует конечный \(\displaystyle\lim_{k \rightarrow \infty}S_{n}\). \(\bullet\)
Замечание 2.
Согласно отбрасывание конечного числа членов ряда или добавление конечного числа членов к данному ряду не влияет на его сходимость.
Свойство 3.
Если ряд \(\displaystyle\sum_{n=1}^{\infty}a_{n}\) сходится, то и ряд
$$
\sum_{j=1}^{\infty}b_{j},\label{ref17}
$$
полученный группировкой членов ряда \(\displaystyle\sum_{n=1}^{\infty}a_{n}\) без изменения порядка их расположения, также сходится и имеет ту же сумму, что и ряд \(\displaystyle\sum_{n=1}^{\infty}a_{n}\).
\(\circ\) Пусть \(b_{1} = a_{1} + a_{2} + \ldots + a_{k_{1}}\), \(b_{2} = \displaystyle a_{k_{1} + 1} + a_{k_{1} + 2} + \ldots + a_{k_{2}}\), …, \(b_{j} = a_{k_{j}-1} + \ldots + a_{k_{j}}\) где \(j \in \mathbb{N}\), \(\{k_{j}\}\) — строго возрастающая последовательность натуральных чисел. Обозначим \(S_{n} = \displaystyle\sum_{k=1 }^{n}a_{k}\), \(\sigma_{m} = \displaystyle\sum_{j=1}^{\infty}b_{j}\); тогда \(\sigma_{m} = S_{k_{m}}\). Так как \(\{\sigma_{m}\}\) — подпоследовательность сходящейся последовательности \(S_{1}, S_{2}, \ldots\), то существует \(\displaystyle\lim_{m \rightarrow \infty}\sigma_{m} = S\), где \(S\) — сумма ряда \eqref{ref2}. \(\bullet\)
Как создать кумулятивную диаграмму суммы в Excel (с примером)
В этом руководстве представлен пошаговый пример того, как создать следующую сводную диаграмму в Excel:
Шаг 1: введите данные
Во-первых, давайте создадим следующий набор данных, который показывает общий объем продаж некоторого товара в течение каждого месяца в году:
Шаг 2: Рассчитайте совокупную сумму
Далее мы будем использовать следующую формулу для расчета совокупной суммы продаж:
Мы можем ввести эту формулу в ячейку C2 , а затем скопировать и вставить ее в каждую оставшуюся ячейку в столбце C:
Шаг 3: Создайте гистограмму со средней линией
Затем выделите диапазон ячеек A1:C13 , затем нажмите вкладку « Вставка » на верхней ленте, затем нажмите « Сгруппированный столбец » в группе « Диаграммы ».
Будет создана следующая диаграмма:
Затем щелкните правой кнопкой мыши в любом месте диаграммы и выберите « Изменить тип диаграммы» :
В появившемся новом окне нажмите Combo , а затем нажмите OK :
Диаграмма будет преобразована в гистограмму с линией:
Синие столбцы представляют продажи за каждый месяц, а оранжевая линия — совокупные продажи.
Шаг 4. Настройте диаграмму (необязательно)
Не стесняйтесь добавлять заголовок, настраивать цвета, настраивать стиль линий и настраивать ширину полос, чтобы сделать график более эстетичным:
Простейший график изменений
График нужен тогда, когда необходимо показать изменения данных. Начнем с простейшей диаграммы для демонстрации событий в разные промежутки времени.
Допустим, у нас есть данные по чистой прибыли предприятия за 5 лет:
| Год | Чистая прибыль* |
| 2010 | 13742 |
| 2011 | 11786 |
| 2012 | 6045 |
| 2013 | 7234 |
| 2014 | 15605 |
* Цифры условные, для учебных целей.
Заходим во вкладку «Вставка». Предлагается несколько типов диаграмм:
![]()
Выбираем «График». Во всплывающем окне – его вид. Когда наводишь курсор на тот или иной тип диаграммы, показывается подсказка: где лучше использовать этот график, для каких данных.
![]()
Выбрали – скопировали таблицу с данными – вставили в область диаграммы. Получается вот такой вариант:
![]()
Прямая горизонтальная (синяя) не нужна. Просто выделяем ее и удаляем. Так как у нас одна кривая – легенду (справа от графика) тоже убираем. Чтобы уточнить информацию, подписываем маркеры. На вкладке «Подписи данных» определяем местоположение цифр. В примере – справа.
![]()
Улучшим изображение – подпишем оси. «Макет» – «Название осей» – «Название основной горизонтальной (вертикальной) оси»:
![]()
Заголовок можно убрать, переместить в область графика, над ним. Изменить стиль, сделать заливку и т.д. Все манипуляции – на вкладке «Название диаграммы».
![]()
Вместо порядкового номера отчетного года нам нужен именно год. Выделяем значения горизонтальной оси. Правой кнопкой мыши – «Выбрать данные» — «Изменить подписи горизонтальной оси». В открывшейся вкладке выбрать диапазон. В таблице с данными – первый столбец. Как показано ниже на рисунке:
![]()
Можем оставить график в таком виде. А можем сделать заливку, поменять шрифт, переместить диаграмму на другой лист («Конструктор» — «Переместить диаграмму»).
Как найти?
Чтобы найти сумму ряда нужно выполнить несколько операций над общим членом ряда:
- Составить частичную сумму $ S_n $
- Найти предел $ lim_ S_n = S $
Если получено конечное число $ S $, то оно и есть сумма ряда!
Типы общего члена ряда в задачах:
- Ряд задан бесконечной убывающей геометрической прогрессией $ sum_^infty q^n $, $ |q| lt 1 $ В этом случае сумма вычисляется по формуле $ S = frac<1-q>$, где $ b_1 $ – первый член прогрессии, а $ q $ – её основание
- Ряд задан в виде рациональной дроби $ frac$ Здесь нужно воспользоваться методом неопределенных коэффициентов для разложения дроби на сумму элементарных дробей. Затем составить частичную сумму $ S_n $ и найти её предел, который будем искомой суммой
Графики зависимости
Данные одного столбца (строки) зависят от данных другого столбца (строки).
Построить график зависимости одного столбца от другого в Excel можно так:
![]()
Условия: А = f (E); В = f (E); С = f (E); D = f (E).
Выбираем тип диаграммы. Точечная. С гладкими кривыми и маркерами.
Выбор данных – «Добавить». Имя ряда – А. Значения Х – значения А. Значения У – значения Е. Снова «Добавить». Имя ряда – В. Значения Х – данные в столбце В. Значения У – данные в столбце Е. И по такому принципу всю таблицу.
![]()
Готовые примеры графиков и диаграмм в Excel скачать:
Точно так же можно строить кольцевые и линейчатые диаграммы, гистограммы, пузырьковые, биржевые и т.д. Возможности Excel разнообразны. Вполне достаточно, чтобы наглядно изобразить разные типы данных.
Тригонометрические ряды
- Ряд Фурье для периодической функции с периодом 2π
- Ряд Фурье функции f(x):
- Коэффициенты Фурье:
- Разложение в ряд Фурье четных и нечетных функций с периодом 2π
-
f(-x) = f(x)
ряд Фурье содержит только косинусы кратных дуг: -
f(-x) = -f(x)
ряд Фурье содержит только синусы кратных дуг:
Ряд Фурье для функции с произвольным периодом Т=2l, f(x+2l) = f(x):![]()
где
- Разложение в ряд Фурье непериодических функций, заданных на отрезкеx ∈ или на отрезке x ∈
Произвольная функция f(x) задана на отрезке ; на отрезок она может быть продолжена произвольным образом: – некоторая кусочно-монотонная функция.
Наиболее часто встречающиеся продолжения: -
f1(x)=f(-x), x ∈ (четное продолжение)
где x ∈ n = 0, 1, 2,… -
f1(x) = —f(−x), x ∈
(нечетное продолжение)
где x ∈ n = 1, 2,… - На всю действительную ось ϕ(x) продолжается периодически с периодом 2l, ϕ(x) = ϕ(x + 2l). Функция ϕ(x) разлагается в ряд Фурье, причем в точках x = ±l выполняется условие: где то есть, – левый предел f(x) в точке x = l, – правый предел f(x) в точке x = l.
Как написать знак суммы (количества) в таблицах Excel.
При написании формул в документах MS Excel или Word зачастую возникает потребность в написании математического знака суммы (он же «знак суммирования» или «знак нахождения суммы»). Некоторые далекие от математических исчислений люди называют его «знак количества».
Выглядит знак суммы, как угловатая растянутая относительно горизонтальной оси симметрии заглавная русская буква «Е» или английская «E».
Вставить знак суммы в ячейку таблицы «эксель» или на лист «вордовского» документа можно двумя методами, которые приведены ниже:
При помощи опций на панели быстрого доступа в самой программе.
Как поставить знак суммы при помощи таблицы символов.
![]()
Необходимо последовательно выполнить следующие действия:
- Войти в меню «Пуск» => Программы => Стандартные => Служебные => Таблица символов.
- Выбрать символ суммирования;
- Скопировать символ суммирования;
- Вставить символ в таблицу или документ «Ворда».
Способ нехитрый и не занимает много времени.
Как поставить знак суммы при помощи встроенных возможностей «Эксель».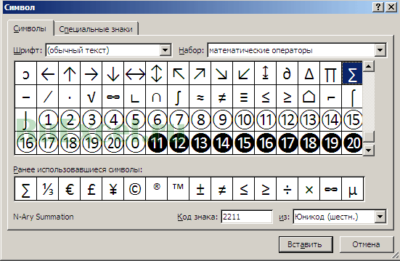
Необходимо выполнить следующую последовательность действий:
- Выбрать ячейку, в которую поставите знак суммы;
- В меню быстрого доступа выбрать вкладку «Вставка»
- Выбрать пиктограмму «Символ»;
- В появившемся окне выбрать знак суммы и вставить его при помощи кнопки «Вставить»
Подробное пошаговое видео о том, как выполняются описанные выше действия:
Ряды с комплексными членами.
Последовательность комплексных чисел \(\{z_{n}\}\) называют сходящейся, если существует такое комплексное число \(z\), что
$$
\lim_{n \rightarrow \infty}|z_{n}-z| = 0,\nonumber
$$
где \(|z|\) — модуль комплексного числа \(z\). В этом случае пишут \(\displaystyle\lim_{n \rightarrow \infty}z_{n} = z\) или \(z_{n} \rightarrow z\) при \(n \rightarrow \infty\).
Если \(z_{n} = x_{n} + iy_{n}\), \(z = x + iy\), то условие \(z_{n} \rightarrow z\) при \(n \rightarrow \infty\) эквивалентно выполнению условий \(x_{n} \rightarrow x\) и \(y_{n} \rightarrow y\) при \(n \rightarrow \infty\).
Ряд с комплексными членами
$$
\sum_{n=1}^{\infty}z_{n},\label{ref21}
$$
называют сходящимся, если существует
$$
\lim_{n \rightarrow \infty} \sum_{k=1 }^{n}z_{k} = S,\nonumber
$$
где \(S \in \mathbb{C}\). В этом случае пишут \(\displaystyle\sum_{n=1}^{\infty}z_{n} = S\), а комплексное число \(S\) называют суммой ряда \eqref{ref21}.










